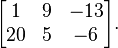Senin, 29 Juni 2015
CARA MEMBUAT GAMBAR BERPUTAR DAN MEMBESAR PADA BLOG

Cara membuat gambarberputar dan membesar pada blog..
cara membuat gambar berputar dan membesar pada blog, cara membuat gambar berputar lincah pada blog, cara memuat gambar berputar bebas pada blog, cara membuat gambar berputar ketika disentuh oleh krusor, cara memperindah tampilan blog dengan memutar gambar, tampilan gambar berputar pada blog, mempercantik blog dengan memutar gambar.
cara membuat gambar berputar dan membesar pada blog, cara membuat gambar berputar lincah pada blog, cara memuat gambar berputar bebas pada blog, cara membuat gambar berputar ketika disentuh oleh krusor, cara memperindah tampilan blog dengan memutar gambar, tampilan gambar berputar pada blog, mempercantik blog dengan memutar gambar.
Cara membuat gambarberputar dan membesar pada blog, mungkin temen-temen bertanya-tanya
dalam hati, bagai manasih caranya agar gambar di blog sobat bisa
berputar-putar, hehehee , , caranya mudah sob, and kalian pasti bisa
karna sangat mudah tentunya,
tujuan memutar gambar pada
blog adalah untuk memper indah / membuat pembaca blog kerasan untuk
berada didalam blog kita, karna menurut mas seem penampilan tu sangat
penting hehehee,,, ya udah deh langsung ja kepokok permasalahannya ya
itu membuat gambar berputardan membesar... cikidot....
Uji Asumsi Klasik (4)
Uji asumsi klasik adalah persyaratan statistik yang harus
dipenuhi pada analisis regresi linear berganda yang berbasis ordinary least
square (OLS). Jadi analisis regresi yang tidak berdasarkan OLS tidak memerlukan
persyaratan asumsi klasik, misalnya regresi logistik atau regresi ordinal.
Demikian juga tidak semua uji asumsi klasik harus dilakukan pada analisis
regresi linear, misalnya uji multikolinearitas tidak dapat dipergunakan pada
analisis regresi linear sederhana dan uji autokorelasi tidak perlu diterapkan
pada data cross sectional.
Uji asumsi klasik juga tidak perlu dilakukan untuk analisis regresi linear yang bertujuan untuk menghitung nilai pada variabel tertentu. Misalnya nilai return saham yang dihitung dengan market model, atau market adjusted model. Perhitungan nilai return yang diharapkan dilakukan dengan persamaan regresi, tetapi tidak perlu diuji asumsi klasik.
Uji Asumsi Klasik (3)
Uji Asumsi Klasik Model Regresi Linier Berganda
Estimasi yang peneliti ciptakan melalui model regresi linier berganda (multiple regression) memberi hubungan antar beberapa variabel. Tapi hasil regresi tidak secara otomatis memberikan hubungan yang handal.
Peneliti harus mengetahui sifat-sifat estimator dan menunjukkan beberapa asumsi dasar di dalam dataset. Sebuah model disebut sebagai model yang baik jika memenuhi beberapa asumsi yang disebut dengan asumsi klasik (classical assumptions).
Peneliti harus mengetahui sifat-sifat estimator dan menunjukkan beberapa asumsi dasar di dalam dataset. Sebuah model disebut sebagai model yang baik jika memenuhi beberapa asumsi yang disebut dengan asumsi klasik (classical assumptions).
Uji Asumsi Klasik (1)
Uji asumsi klasik adalah persyaratan statistik yang harus dipenuhi pada analisis regresi linear berganda
yang berbasis Ordinary Least Square (OLS). Jadi analisis regresi yang
tidak berdasarkan OLS tidak memerlukan persyaratan asumsi klasik,
misalnya regresi logistik atau regresi ordinal.
Demikian juga tidak semua uji asumsi klasik harus dilakukan pada
analisis regresi linear, misalnya uji multikolinearitas tidak dilakukan
pada analisis regresi linear sederhana dan uji autokorelasi tidak perlu
diterapkan pada data cross sectional.
Uji asumsi klasik juga tidak perlu dilakukan untuk analisis regresi
linear yang bertujuan untuk menghitung nilai pada variabel tertentu.
Misalnya nilai return saham yang dihitung dengan market model, atau
market adjusted model. Perhitungan nilai return yang diharapkan dapat
dilakukan dengan persamaan regresi, tetapi tidak perlu diuji asumsi
klasik.
Uji asumsi klasik yang sering digunakan yaitu uji multikolinearitas, uji
heteroskedastisitas, uji normalitas, uji autokorelasi dan uji
linearitas. Tidak ada ketentuan yang pasti tentang urutan uji mana dulu
yang harus dipenuhi. Analisis dapat dilakukan tergantung pada data yang
ada. Sebagai contoh, dilakukan analisis terhadap semua uji asumsi
klasik, lalu dilihat mana yang tidak memenuhi persyaratan. Kemudian
dilakukan perbaikan pada uji tersebut, dan setelah memenuhi persyaratan,
dilakukan pengujian pada uji yang lain.
Kamis, 25 Juni 2015
PENGERTIAN DAN JENIS-JENIS MATRIKS
Matriks adalah susunan kumpulan bilangan yang diatur dalam baris dan
kolom berbentuk persegi panjang. Matriks dicirikan dengan elemen-elemen
penyusun yang diapit oleh tanda kurung siku [ ] atau tanda kurung biasa (
). Ukuran sebuah matriks dinyatakan dalam satuan ordo, yaitu banyaknya
baris dan kolom dalam matriks tersebut. Ordo merupakan karakteristik
suatu matriks yang menjadi patokan dalam operasi-operasi antar matriks.
Memahami ordo matriks merupakan hal yang penting karena cukup banyak
terjadi kesalahan dalam mengerjakan soal-soal matriks yang disebabkan
oleh kekeliruan dalam memahami ordo matriks. Ketika seorang murid
mengartikan ordo secara terbalik yaitu kolom dikali baris tentu hasilnya
akan sangat berbeda. Matriks umumnya disimbolkan seperti berikut ini:
Matriks
Dalam matematika, matriks adalah kumpulan bilangan, simbol, atau ekspresi, berbentuk persegi panjang yang disusun menurut baris dan kolom. Bilangan-bilangan yang terdapat di suatu matriks disebut dengan elemen atau anggota matriks. Contoh matriks dengan 2 baris dan 3 kolom yaitu:
Pemanfaatan matriks misalnya dalam menemukan solusi sistem persamaan linear. Penerapan lainnya adalah dalam transformasi linear, yaitu bentuk umum dari fungsi linear, misalnya rotasi dalam 3 dimensi.
Matriks seperti halnya variabel biasa dapat dimanipulasi, seperti
dikalikan, dijumlah, dikurangkan dan didekomposisikan. Dengan
representasi matriks, perhitungan dapat dilakukan dengan lebih
terstruktur.
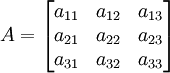
Rabu, 24 Juni 2015
SAP Matematika Ekonomi II
Mata Kuliah : Matematika Ekonomi II
Jurusan/Program Studi : S1 / Ilmu Ekonomi
Semester/Jumlah SKS : 2/3
Deskripsi Singkat:
Mencakup pengetahuan dasar mengenai differensial, integral, matrik serta penerapannya dalam ilmu ekonomi.
Standar Kompetensi:
Mahasiswa mampu menerapkan kaidah dasar matematika sebagai alat bantu untuk lebih memahami ilmu ekonomi dan aplikasinya.
Rincian Materi Perkuliahan Tiap Pertemuan:
Pertemuan 1 : Differensial Fungsi Majemuk
Pertemuan 2 : Differensial Fungsi Majemuk (lanjutan)
Pertemuan 3 : Penerapan ekonomi Differensial Fungsi Majemuk
Pertemuan 4 : Integral Taktentu
Pertemuan 5 : Penerapan Ekonomi Integral Tak tentu
Pertemuan 6 : Integral tertentu
Pertemuan 7 : Penerapan Ekonomi Integral tertentu
UTS
Pertemuan 8 : Matriks
Pertemuan 9 : Matriks (lanjutan)
Pertemuan 10 : Analisis Masukan Keluaran
Pertemuan 11 : Analisis Masukan Keluaran (lanjutan)
Pertemuan 12 : Programasi Linier
Pertemuan 13 : Programasi Linier (lanjutan)
Pertemuan 14 : Review materi
UAS
Kepustakaan:
1.Dumairy , 1999, Matematika terapan untuk bisnis dan ekonomi, BPFE, Yogyakarta.
2.Alpha C.Chiang, 2006, Dasar-dasar Matematika Ekonomi Jilid 2, Penerbit Erlangga, Jakarta
Jurusan/Program Studi : S1 / Ilmu Ekonomi
Semester/Jumlah SKS : 2/3
Deskripsi Singkat:
Mencakup pengetahuan dasar mengenai differensial, integral, matrik serta penerapannya dalam ilmu ekonomi.
Standar Kompetensi:
Mahasiswa mampu menerapkan kaidah dasar matematika sebagai alat bantu untuk lebih memahami ilmu ekonomi dan aplikasinya.
Rincian Materi Perkuliahan Tiap Pertemuan:
Pertemuan 1 : Differensial Fungsi Majemuk
Pertemuan 2 : Differensial Fungsi Majemuk (lanjutan)
Pertemuan 3 : Penerapan ekonomi Differensial Fungsi Majemuk
Pertemuan 4 : Integral Taktentu
Pertemuan 5 : Penerapan Ekonomi Integral Tak tentu
Pertemuan 6 : Integral tertentu
Pertemuan 7 : Penerapan Ekonomi Integral tertentu
UTS
Pertemuan 8 : Matriks
Pertemuan 9 : Matriks (lanjutan)
Pertemuan 10 : Analisis Masukan Keluaran
Pertemuan 11 : Analisis Masukan Keluaran (lanjutan)
Pertemuan 12 : Programasi Linier
Pertemuan 13 : Programasi Linier (lanjutan)
Pertemuan 14 : Review materi
UAS
Kepustakaan:
1.Dumairy , 1999, Matematika terapan untuk bisnis dan ekonomi, BPFE, Yogyakarta.
2.Alpha C.Chiang, 2006, Dasar-dasar Matematika Ekonomi Jilid 2, Penerbit Erlangga, Jakarta